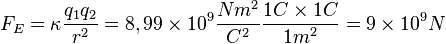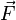 dada por la siguiente ecuación:
dada por la siguiente ecuación:(1)En los modelos relativistas actuales, el campo eléctrico se incorpora, junto con el campo magnético, en campo tensorial cuadridimensional, denominado campo electromagnético Fμν.[2]
Los campos eléctricos pueden tener su origen tanto en cargas eléctricas como en campos magnéticos variables. Las primeras descripciones de los fenómenos eléctricos, como la ley de Coulomb, sólo tenían en cuenta las cargas eléctricas, pero las investigaciones de Michael Faraday y los estudios posteriores de James Clerk Maxwell permitieron establecer las leyes completas en las que también se tiene en cuenta la variación del campo magnético.
Esta definición general indica que el campo no es directamente medible, sino que lo que es observable es su efecto sobre alguna carga colocada en su seno. La idea de campo eléctrico fue propuesta por Faraday al demostrar el principio de inducción electromagnética en el año 1832.
La unidad del campo eléctrico en el SI es Newton partido de culombio (N/C), voltio partido de metro (V/m) o, en unidades básicas, kg·m·s−3·A−1.
La definición más intuitiva acerca del campo eléctrico se la puede estudiar mediante la ley de Coulomb. Esta ley, una vez generalizada, permite expresar el campo entre distribuciones de carga en reposo relativo. Sin embargo, para cargas en movimiento se requiere una definición más formal y completa acerca del campo requiere el uso de cuadrivectores y el principio de mínima acción. A continuación se describen ambas.
[editar] Definición mediante la ley de Coulomb
Partiendo de la ley de Coulomb que expresa que la fuerza entre dos cargas en reposo relativo depende del cuadrado de la distancia, matemáticamente es igual a:[1]
Donde:
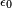 es la permitividad eléctrica del vacío tiene que ver con el sistema internacional,
es la permitividad eléctrica del vacío tiene que ver con el sistema internacional, son las cargas que interactúan,
son las cargas que interactúan,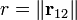 es la distancia entre ambas cargas,
es la distancia entre ambas cargas, , es el vector de posición relativa de la carga 2 respecto a la carga 1.
, es el vector de posición relativa de la carga 2 respecto a la carga 1.
 es el unitario en la dirección
es el unitario en la dirección 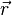 . Nótese que en la fórmula se está usando ε0, esta es la permeabilidad en el vacío. Para calcular la interacción en otro medio es necesario cambiar la permeabilidad de dicho medio. (ε = εr.ε0)
. Nótese que en la fórmula se está usando ε0, esta es la permeabilidad en el vacío. Para calcular la interacción en otro medio es necesario cambiar la permeabilidad de dicho medio. (ε = εr.ε0)La ley anterior presuponía que la posición de una partícula en un instante dado, hace que su campo eléctrica afecte en el mismo instante a cualquier otra carga. Ese tipo de interacciónes en las que el efecto sobre el resto de partículas parece dependender sólo de la posición de la partícula causante sin importar la distancia entre las partículas se denomina en física acción a distancia. Si bien la noción de acción a distancia fue aceptada inicialmente por el propio Newton, experimentos más cuidados a lo largo del siglo XIX llevaron a desechar dicha noción como no-realista. En ese contexto se pensó que el campo eléctrico no sólo era un artificio matemático sino un ente físico que se propaga a una velocidad finita (la velocidad de la luz) hasta afectar a otras partículas. Esa idea conllevaba modificar la ley de Coulomb de acuerdo con los requerimientos de la teoría de la relatividad y dotar de entidad física al campo eléctrico.[1] Así, el campo eléctrico es una distorsión electromagnética que sufre el espacio debido a la presencia de una carga. Considerando esto se puede obtener una expresión del campo eléctrico cuando este sólo depende de la distancia entre las cargas:
Donde claramente se tiene que
 , la que es una de las definiciones más conocidas acerca del campo eléctrico.
, la que es una de las definiciones más conocidas acerca del campo eléctrico.[editar] Definición formal
La definición más formal de campo eléctrico, válida también para cargas moviéndose a velocidades cercanas a la de la luz, surge a partir de calcular la acción de una partícula cargada en movimiento a través de un campo electromagnético.[2] Este campo forma parte de un único campo electromagnético tensorial Fμν definido por un potencial cuadrivectorial de la forma:[1](1)donde φ es el potencial escalar y
 es el potencial vectorial tridimensional. Así, de acuerdo al principio de mínima acción, se plantea para una partícula en movimiento en un espacio cuadridimensional:
es el potencial vectorial tridimensional. Así, de acuerdo al principio de mínima acción, se plantea para una partícula en movimiento en un espacio cuadridimensional:(2)donde e es la carga de la partícula, m es su masa y c la velocidad de la luz. Reemplazando () en () y conociendo que dxi = uids, donde dxi es el diferencial de la posición definida dxi = (cdt,dx,dy,dz) y ui es la velocidad de la partícula, se obtiene:
(3)El término dentro de la integral se conoce como el lagrangiano del sistema; derivando esta expresión con respecto a la velocidad se obtiene el momento de la partícula, y aplicando las ecuaciones de Euler-Lagrange se encuentra que la variación temporal de la cantidad de movimiento de la partícula es:
(4)De donde se obtiene la fuerza total de la partícula. Los dos primeros términos son independientes de la velocidad de la partícula, mientras que el último depende de ella. Entonces a los dos primeros se les asocia el campo eléctrico y al tercero el campo magnético. Así se encuentra la definición más general para el campo eléctrico:[2]
(5)La ecuación () brinda mucha información acerca del campo eléctrico. Por un lado, el primer término indica que un campo eléctrico es producido por la variación temporal de un potencial vectorial descrito como
 donde
donde 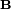 es el campo magnético; y por otro, el segundo representa la muy conocida descripción del campo como el gradiente de un potencial.[2]
es el campo magnético; y por otro, el segundo representa la muy conocida descripción del campo como el gradiente de un potencial.[2]
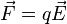
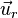 por una distribucion de carga
por una distribucion de carga  .
.
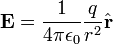

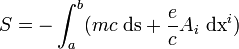



 de la fuerza que cada una de las dos cargas puntuales
de la fuerza que cada una de las dos cargas puntuales 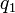 y
y  ejerce sobre la otra separadas por una distancia
ejerce sobre la otra separadas por una distancia  se expresa como:
se expresa como: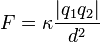

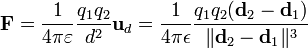
 es un
es un 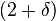 , entonces
, entonces 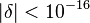 .
.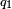 y
y  . La ley de Coulomb es una ecuación vectorial e incluye el hecho de que la fuerza actúa a lo largo de la línea de unión entre las cargas.
. La ley de Coulomb es una ecuación vectorial e incluye el hecho de que la fuerza actúa a lo largo de la línea de unión entre las cargas.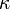 es la
es la 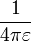
 donde
donde 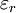 es la
es la  , y
, y 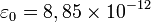
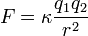
 tal que la fuerza dada por la ley de Coulomb sea expresable como:
tal que la fuerza dada por la ley de Coulomb sea expresable como:
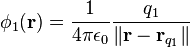
 , es el vector posición genérico de un punto donde se pretende definir el potencial de Coulomb y
, es el vector posición genérico de un punto donde se pretende definir el potencial de Coulomb y , es el vector de posición de la carga eléctrica
, es el vector de posición de la carga eléctrica  cuyo campo pretende caracterizarse por medio del potencial.
cuyo campo pretende caracterizarse por medio del potencial.
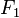 . En el equilibrio:
. En el equilibrio:
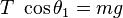
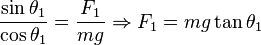
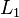 la separación de equilibrio entre las esferas cargadas, la fuerza
la separación de equilibrio entre las esferas cargadas, la fuerza  y, por lo tanto, se cumple la siguiente igualdad:
y, por lo tanto, se cumple la siguiente igualdad: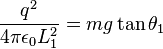
 y la fuerza de repulsíón entre las mismas estará dada por:
y la fuerza de repulsíón entre las mismas estará dada por: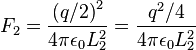
 . Y de modo similar se obtiene:
. Y de modo similar se obtiene: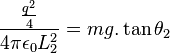
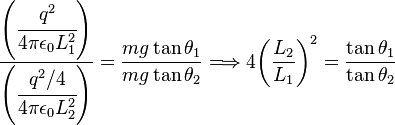
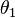 y
y  y las separaciones entre las cargas
y las separaciones entre las cargas 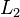 es posible verificar que la igualdad se cumple dentro del error experimental. En la práctica, los ángulos pueden resultar difíciles de medir, así que si la longitud de los hilos que sostienen las esferas son lo suficientemente largos, los ángulos resultarán lo bastante pequeños como para hacer la siguiente aproximación:
es posible verificar que la igualdad se cumple dentro del error experimental. En la práctica, los ángulos pueden resultar difíciles de medir, así que si la longitud de los hilos que sostienen las esferas son lo suficientemente largos, los ángulos resultarán lo bastante pequeños como para hacer la siguiente aproximación:
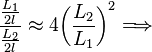
![\frac{L_1}{L_2}\approx 4 {\left ( \frac {L_2}{L_1} \right ) }^2\Longrightarrow \frac{L_1}{L_2}\approx\sqrt[3]{4} \,\!](http://upload.wikimedia.org/math/7/c/e/7cef359a7cd4a5f6a3be9d150a4a14e0.png)
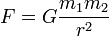
 la
la  las masas de los cuerpos en cuestión y
las masas de los cuerpos en cuestión y la distancia entre los centros de las masas.
la distancia entre los centros de las masas. y
y 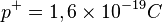 respectivamente y sus masas son
respectivamente y sus masas son  y
y  . Sustituyendo los datos:
. Sustituyendo los datos:
 .
.